Stability of steady-state equilibrium for overlapping generation model

This is a summary of discussion with Alecos Papadopoulos at http://economics.stackexchange.com/questions/16118/stability-of-steady-state-equilibrium-for-overlapping-generation-model as well as from what I learnt and thought in my graduate macroeconomics class.

  • In draft edition of Daron Acemoglu's Introduction to Modern Economic Growth (2007), proposition 9.4 which states that:
    In the overlapping-generations model with two-period lived households, Cobb-Douglas technology and CRRA preferences, there exists a unique steady-state equilibrium with the capital-labor ratio k* given by (9.15) and as long as $\theta \geq 1$, this steady-state equilibrium is globally stable for all k (0) > 0.
    has a typo. In 2009 edition of the textbook, proposition 9.4 is corrected to:
    In the overlapping-generations model with two-period lived households, Cobb-Douglas technology and CRRA preferences, there exists a unique steady-state equilibrium with the capital-labor ratio k* given by (9.15) and for any $\theta$ > 0, this steady-state equilibrium is globally stable for all k (0) > 0.

  • In the following, we will use the setup and symbol of overlapping-generations model with two-period lived households, Cobb-Douglas technology and CRRA preferences as in Daron Acemoglu's Introduction to Modern Economic Growth (2009).
    To show $\theta > 0$ is the condition for stable steady-state equilibrium for overlapping generation model, we use formula (9.17) derived in the textbook: $$k(t+1)=\frac{(1-\alpha)k(t)^\alpha}{(1+n)[1+\beta^{-\frac{1}{\theta}}(\alpha k(t+1)^{\alpha-1})^{\frac{\theta-1}{\theta}}]}$$ We can rearrange to get: $$ k(t)=\big[ \frac{1+n}{1-\alpha} [k(t+1)+\beta^{-\frac{1}{\theta}}\alpha^{\frac{\theta-1}{\theta}}k(t+1)^{(\alpha-1)(1-\frac{1}{\theta})+1}] \big]^\frac{1}{\alpha} \text{ .....(1)} $$
    • Case $\theta = 0$:
      Note that when the textbook derives (9.17), it implicitly assumes that $\theta \neq 0$ (for derivation of Euler equation for consumption in P.333 of 2009 edition of the textbook). When $\theta = 0$, equation (1) no longer applies. Returning to the utility maximization problem with $\theta = 0$: $$ \text{max } U(t) = c_1(t) + \beta(c_2(t+1)) \text{ such that } c_1(t) + \frac{c_2(t+1)}{R(t+1)} = w(t) \\ \Leftrightarrow \text{max } U(t) = c_1(t) + \beta(w(t) - c_1(t))R(t+1) $$
      • Wrong version (Treat utility maximization problem as central-planner problem):
        $$ \text{max } U(t) = c_1(t) + \beta(w(t) - c_1(t))R(t+1) \\ = c_1(t) + \beta(w(t) - c_1(t))f'(k(t+1)) \text{ ...Wrong to set $R(t+1) = f'(k(t+1))$, treating it as central-planner problem} \\ = c_1(t) + \beta(w(t) - c_1(t))\alpha k(t+1)^{\alpha - 1} \\ = c_1(t) + \beta(w(t) - c_1(t))\alpha (\frac{s(t)}{1+n})^{\alpha - 1} \text{ (Given full capital depreciation)}\\ = c_1(t) + \beta s(t) \alpha (\frac{s(t)}{1+n})^{\alpha - 1} \\ = w(t) - s(t) + \frac{\alpha\beta}{(1+n)^{\alpha - 1}} s(t)^\alpha \\ $$ First-order condition with respect to $s(t)$ gives: $$ s(t)^* = (1+n)(\alpha^2 \beta)^{\frac{1}{1 - \alpha}} $$ Then, $$ k(t+1) = \frac{s(t)}{1+n} = (\alpha^2 \beta)^{\frac{1}{1 - \alpha}}\text{ , which is a constant} $$ This means that the steady-state equilibrium where $k^* = (\alpha^2 \beta)^{\frac{1}{1 - \alpha}}$ is globally stable as even k deviates from $k^*$ for one period, next period k will return to steady state $k^*$.
      • Correct version (To be confirmed):
        $$ \text{max } U(t) = c_1(t) + \beta(w(t) - c_1(t))R(t+1) \\ = c_1(t) (1 - \beta R(t+1)) + \beta R(t+1)w(t) \text{ ...Should treat R(t+1) as given as consumer's own optimization problem}\\ $$ s(t) has to be non-negative for $k(t+1)= \frac{s(t)}{1+n}$ and k(t+1) is non-negative. $$ c_1(t)^* = \begin{cases} w(t)\text{, for }\beta R(t+1) <1 \\ [0, w(t)]\text{, for }\beta R(t+1) = 1 \\ 0\text{, for }\beta R(t+1) > 1 \\ \end{cases} $$ $$ s(t)^* = \begin{cases} 0\text{, for }\beta R(t+1) <1 \\ w(t) - c_1(t)^* \in [0, w(t)]\text{, for }\beta R(t+1) = 1 \\ w(t)\text{, for }\beta R(t+1) > 1 \\ \end{cases} $$ For $R(t+1) = f'(k(t+1)) = \alpha k(t+1)^{\alpha - 1}$, $$ k(t+1) = \frac{s(t)}{1+n} = \begin{cases} 0\text{, for }\beta R(t+1) <1 \Leftrightarrow k(t+1) < (\alpha \beta)^{\frac{1}{1 - \alpha}} \\ \frac{w(t) - c_1(t)}{1+n} \in [0, \frac{w(t)}{1+n}]\text{, for }\beta R(t+1) = 1 \Leftrightarrow k(t+1) = (\alpha \beta)^{\frac{1}{1 - \alpha}}\\ \frac{w(t)}{1+n} = \frac{k(t)^\alpha - k(t)\alpha k(t)^{\alpha -1}}{1+n} = \frac{1-\alpha}{1+n}k(t)^\alpha\text{, otherwise} \Leftrightarrow k(t) > [\frac{1+n}{1 - \alpha} (\alpha \beta)^{\frac{1}{1 - \alpha}}]^{\frac{1}{\alpha}} \\ \end{cases} $$
        • Original wrong derivation:
          From this, we can draw the following graph:
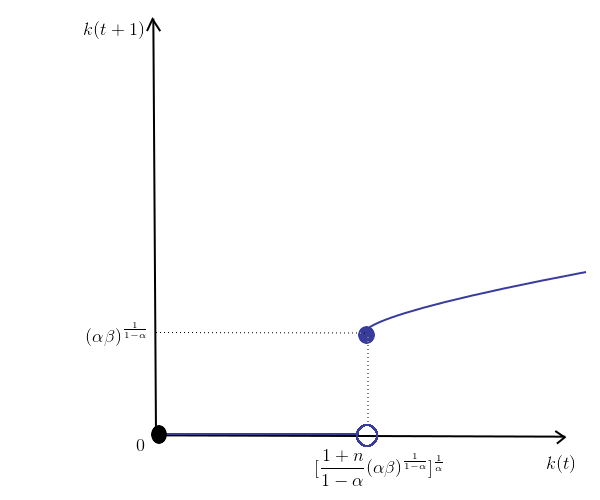
          The blue line is: $$ k(t+1) = \begin{cases} \frac{1-\alpha}{1+n}k(t)^\alpha\text{, for }k(t) \geq [\frac{1+n}{1 - \alpha} (\alpha \beta)^{\frac{1}{1 - \alpha}}]^{\frac{1}{\alpha}} \\ 0\text{, otherwise} \end{cases} $$ For $\frac{1-\alpha}{1+n} k(t)^\alpha = k(t)$, $k(t) = [\frac{1-\alpha}{1+n}]^{\frac{1}{1-\alpha}}$ i.e. blue line crosses the 45-degress line when $k(t) = [\frac{1-\alpha}{1+n}]^{\frac{1}{1-\alpha}}$. $$ D = [\frac{1+n}{1 - \alpha} (\alpha \beta)^{\frac{1}{1 - \alpha}}]^{\frac{1}{\alpha}} - [\frac{1-\alpha}{1+n}]^{\frac{1}{1-\alpha}} \\ = \frac{1+n}{1-\alpha}^{\frac{1}{\alpha}}[(\alpha \beta)^{\frac{1}{\alpha (1-\alpha)}} - (\frac{1+n}{1-\alpha})^{\frac{-1}{(1-\alpha)\alpha}}] $$
          • Case 1: $D > 0 \Leftrightarrow \alpha > \frac{1}{1+(1+n)\beta}$
            We can draw the following graph:
            The red line is 45-degrees line. It can be seen that for all $k > 0$, k will converge to steady-state S k* = 0. The steady-state equilibrium is globally stable.
          • Case 2: $D = 0 \Leftrightarrow \alpha = \frac{1}{1+(1+n)\beta}$
            We can draw the following graph:
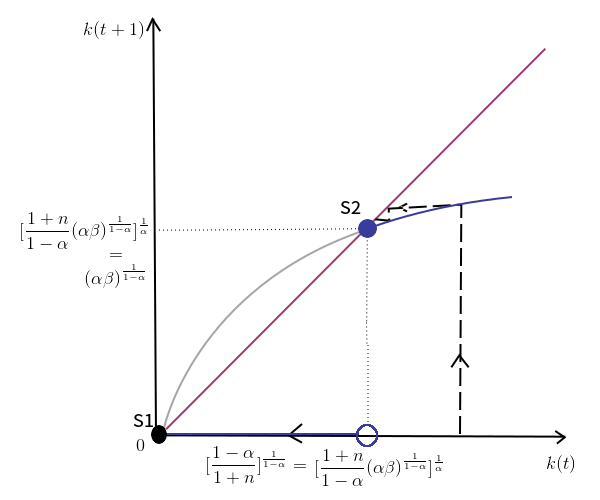            The red line is 45-degrees line. It can be seen that for all $0 < k < [\frac{1-\alpha}{1+n}]^{\frac{1}{1-\alpha}}$, k will converge to steady-state S1 k* = 0 while for all $k \geq [\frac{1-\alpha}{1+n}]^{\frac{1}{1-\alpha}}$, k will converge to steady-state S2 k* = $(\alpha \beta)^{\frac{1}{1-\alpha}}$. The steady-state equilibria are not globally stable.
          • Case 3: $D < 0 \Leftrightarrow \alpha < \frac{1}{1+(1+n)\beta}$
            We can draw the following graph:
            The red line is 45-degrees line. It can be seen that for all $0 < k < [\frac{1+n}{1 - \alpha} (\alpha \beta)^{\frac{1}{1 - \alpha}}]^{\frac{1}{\alpha}}$, k will converge to steady-state S1 k* = 0 while for all $k \geq [\frac{1+n}{1 - \alpha} (\alpha \beta)^{\frac{1}{1 - \alpha}}]^{\frac{1}{\alpha}}$, k will converge to steady-state S2 k* = $[\frac{1-\alpha}{1+n}]^{\frac{1}{1-\alpha}}$. The steady-state equilibria are not globally stable.
        • Correct derivation:
          • Case 1: $\beta R(t+1) < 1 \Leftrightarrow R(t+1) < \frac{1}{\beta}$:
            As the production function $f(k)$ is Cobb-Douglas, it satisfies the Inada condition: $lim_{k(t) \to 0} f'(k(t)) = \infty$. But as $f'(k(t)) = R(t)$, $lim_{k(t) \to 0} R(t) < \infty$ for $R(t) < \frac{1}{\beta} < \infty$ as $\beta \in (0,1)$, violating the Inada condition. This contradiction means this case is impossible.
          • Case 2: $\beta R(t+1) = 1 \Leftrightarrow \beta \alpha k(t+1)^{\alpha-1} = 1 \Leftrightarrow k(t+1)^{\alpha-1} = \frac{1}{\alpha \beta} \Leftrightarrow k(t+1)^{1-\alpha} = \alpha \beta$:
            Denote saving rate at t as $\mathcal{S}(t) = \frac{s(t)}{w(t)}$. $k(t+1) = \frac{s(t)}{1+n} = \frac{\mathcal{S}(t)w(t)}{1+n} = \frac{\mathcal{S}(t)(1-\alpha)k(t)^\alpha}{1+n}$. At steady state, $k^* = \frac{\mathcal{S}^*(1-\alpha){k^*}^\alpha}{1+n}$, meaning $\mathcal{S}^* = \frac{1+n}{1-\alpha}{k^*}^{1-\alpha} = \frac{1+n}{1-\alpha} \alpha \beta$. For $\mathcal{S}^* > 1 \Leftrightarrow (1+n)\alpha\beta > 1 - \alpha \Leftrightarrow \beta > \frac{1 - \alpha}{\alpha (1+n)}$, which is possible. As saving rate cannot be larger than 1, this contradiction means this case is impossible.
          • Case 3: $\beta R(t+1) > 1$:
            This case is possible. $$ k(t+1) = \frac{1-\alpha}{1+n} k(t)^\alpha $$ We can draw the graph:
            The red line is 45-degrees line. The blue line is $k(t+1) = \frac{1-\alpha}{1+n} k(t)^\alpha$ where $0 < \alpha < 1$. For all k(0) > 0, k will converge to steady state $k^* = \frac{1-\alpha}{1+n} {k^*}^\alpha \Leftrightarrow k^* = [\frac{1-\alpha}{1+n}]^{\frac{1}{1-\alpha}}$. The steady-state equilibrium is globally stable.
            TODO: investigate why proposition in textbook not relax the condition of globally stable steady-state equilibrium to $\theta \geq 0$
    • Case $\theta > 0$:
      • Informal way: Let $n = 0.01$, $\alpha = 0.25$, $\beta = 0.75$.
        If $\theta > 0$, we can plot a graph like this$^{[1]}$:
        The blue line is equation (1) where $\theta = 1$ and the red line is 45-degrees line. It can be seen that for all k > 0, k will converge to steady-state k*. The steady-state equilibrium is globally stable.
    • Case $\theta < 0$:
      • Informal way: Let $n = 0.01$, $\alpha = 0.25$, $\beta = 0.75$.
        If $\theta < 0$, we can plot a graph like this$^{[1]}$:
        The blue line is equation (1) where $\theta = -1$ and the red line is 45-degrees line. It can be seen that for some k > 0, k will not converge to steady-state k*. The steady-state equilibrium is not globally stable.
  • TODO: discuss intuition
  • Formal proof of the proposition can be found in Michael Peters and Alp Simsek's Solutions Manual for "Introduction to Modern Economic Growth" - Answer for Exercise 9.6.
  • Acknowledgement: [1] The graphs are modified from those generated by Wolframalpha.

Comments

Post a Comment

Popular posts from this blog

Latex memo

Image
Numbering equations in align environment In align environment, all equations are numbered by default, use \nonumber to make equation on the same line not numbered. Example: Code: \documentclass{article} \usepackage{amsmath} \begin{document} \begin{align} \frac{w^* +\delta V_u^1}{r + \delta} &= V_u^{0} \nonumber \\ w^* &= r V_u^1 - \frac{b(r + \delta)}{1 + r} \end{align} \end{document} Result: In align* environment, all equations are not numbered by default, how about we want to make one equation numbered? Is there any analog of \nonumber? From Ian Thompson at https://tex.stackexchange.com/questions/42726/align-but-show-one-equation-number-at-the-end , we can add the following command before the document begins: \newcommand\numberthis{\addtocounter{equation}{1}\tag{\theequation}} % From Ian Thompson at https://tex.stackexchange.com/questions/42726/align-but-show-one-equation-number-at-the-end Then, we can use \numberthis to make equation on the same line numbered in ...
Keep reading

Linux memo

Convert pdf to png (one page of pdf, one png): pdftoppm -png [pdf file name] [png file name prefix] From https://askubuntu.com/a/50180 Convert all jpg in one directory to pdf (one jpg, one page of pdf): convert *.jpg [Output pdf name] Combine multiple pdf to one pdf: pdftk [First pdf name] ... [Last pdf name] cat output [Output pdf name]
Keep reading